|
|
这道题目要求B结点的位移,如果不考虑材料变形,则BC杆轴力为0,但如果考虑变形,而且题目要求是“变形微小”,那么如何确定BC杆的轴力及变形N=?、ΔL=?这是一道考注册基础课的复习题,请问力学高手应该如何解答这题?
6 n V& ]' j- l: e# ]0 Y
0 N1 f8 X: L, w r+ N% R7 X6 v* l
& g8 G" ^$ G3 z b$ g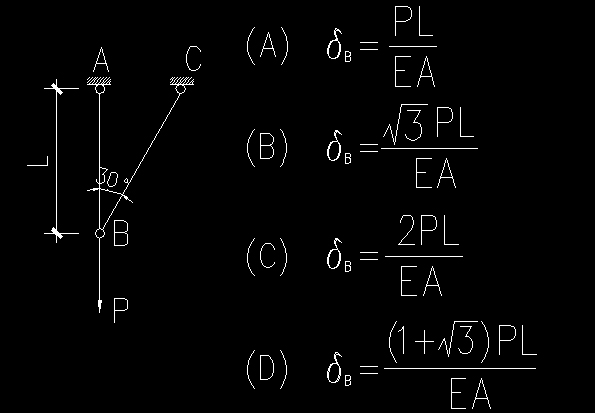 " J* D2 M( O: c2 _4 \/ M " J* D2 M( O: c2 _4 \/ M
% P7 G6 z/ ~* K|||
9 f9 @! Q2 h% Z" L2 F) x- O, q6 G6 R 俺列变形协调方程算了半天,也没有算出来。所以只有蒙一下了。大概选择D吧? 6 C& @! V$ F" g# l: B, O% H7 k0 i
|||1 L8 x1 p2 h) ]( q* U/ p- d
tiuc,书上的答案是(C),但我怎么也想不通为什么选2倍。难道是答案错了?
) Q8 u7 u) v) M# z|||
: C/ r' G1 _9 X1 [# W* j# _, ] 此题答案明显错误!1、若按标准答案,则BC杆轴力的竖向分量的大小为P,与荷载平衡,由平衡方程,则AB杆的轴力为零,明显与事实不符。2、从题目分析,BC杆就是零杆,不论是否考虑微变形。3、从力学模型来看,不论哪种分析方法,结果不会相差很大,BC杆即使有轴力存在,也接近于零,不会达到2/1.732。4、此题答案对应的正确图形:AB杆应为水平杆。
5 \ p5 q2 y7 M- i5 a& b|||
( F: b+ Z8 D" x6 K" U 不考虑答案是否正确,如果在考试中遇到这题,你会选哪一项呢? 9 S6 M5 K4 t- }( d5 _- n% [
|||% |+ D y9 k! L5 r; @# V
如果考虑变形,BC怎么会是零杆?材料力学是忘得差不多了,感觉C应该是不对的。我选根号3减1。 6 r( x) H7 }+ Z1 W
|||
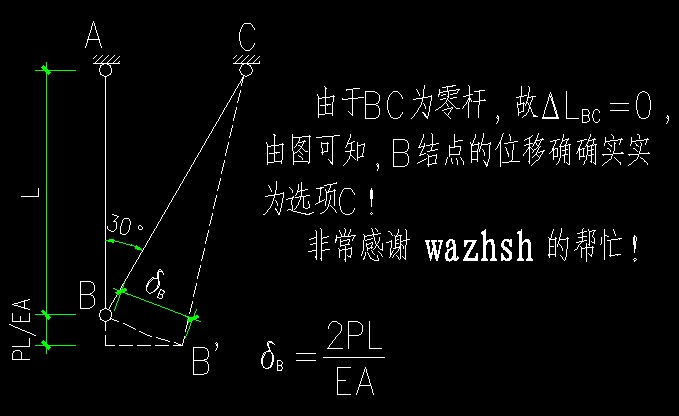
4 J% M6 W; v. L 这道题不知是叮当误会了题目的意思还是我们误会了叮当的意思。现提供我的二次解答(大概是正确的):BC杆的轴力为零,BC杆的伸长为零,但B点的位移确确实实为2PL/EA,方向右向下60度,因此,该题是问B点的位移(与答案下标吻合),而不是问BC杆伸长多少。大家可以根据位移相容(AB杆伸长PL/EA)得到此答案。所以答案是(C)。
3 j; `# _& `: |( D|||
+ ?4 N5 _% x3 n8 i/ i- _9 N: d) | Thank ) P% W; H' w9 e' @
; y- K# A) r4 z' |4 F: |1 w( J) D) L/ N1 k& x% v7 b8 |- x z
 0 j% t% @8 e+ j5 ~ 0 j% t% @8 e+ j5 ~
( y* { U5 k( v, I, I/ H- @
|||
8 A4 z+ v" i0 e2 s0 D 没错,是这个答案,这些题目在课本上有阿,还是很浅的,我们期末考的就难多了,为什么搞了几年施工就会忘记以前的知识,还是你更本没有毕业阿? , T$ n/ S- ^) g/ F+ `: ?, S
|||, n5 u2 H$ F( P) [( G3 }
关键的问题是:此变形必须是微小的,否则bc杆不可能为0杆!
/ N4 f) V8 {" @; v0 X|||
6 \8 P/ E+ X. ^# h; K7 t! n- _$ R 此题大约可用结构力学虚位移原理解。先假设向下作用p=1 得位移PL/EA.再假设向右作用p=1 得位移1.73PL/EA ??两者组合。
X j( H5 a4 Q( M& R|||
4 }9 |" ~+ ]0 c! @+ P 为什么BC是0杆?我刚学材料力学请教请教! # @& t+ z, }! A% o) d1 R$ a
|||' l! R. ?3 W" T2 m6 C
BC杆应该不是零杆,楼上的说得对,材料力学中是这样的:如果BC杆不受外力P作用,那它应该是零杆,可是现在它明显收力了啊???不懂,请高手指明其所以然\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"\\\"--------------------------------------------------------------你在黎明看风景,我在黄昏望着你;你可知道,你就是我唯一的风景!!
7 l/ d, |( i" O+ b% e* M, }|||. ~/ j+ n1 m, S# t1 \
取节点B为隔离体就知道BC为零杆了。。。 ( {* E0 M# b1 [, \
|||- }. F7 r- i7 ?. l: u0 d
不好意思哦是0杆好好学习,天天向上感谢前辈指点
- E$ i- l* X0 L8 w8 T! |* Z|||: U% i( b9 n) Y; d
力学世界中确实有很多很微妙的东西,望爱好力学的朋友经常交流!
( } j1 p$ G2 |7 A6 j& F|||
4 W% Z. t. H- O; t+ o; G 零杆的概念在理论力学中就介绍过了,而且这是材料力学中的一道题。当时我们是当例题讲的。 7 U% I* B1 K/ ~6 x9 e' k
|||
" w/ A; G5 R/ L+ L7 @0 a 不明白 它怎么不向另一方向位移?
2 ^0 M, x5 g5 |: p" v3 O! X& k|||
/ @' m* t# B( R' H) z& p 斜杆不是0杆 . X! @% D" V2 d- X7 `8 D' E
|||. T# I7 F& j+ {( E5 _; v
我认为bc 杆肯定不是0杆。楼上有一位说明了b 点的位移方向是向右下,这个可能大家都是同意的。在这种情况下如果再区b点为隔离体,就回发现ab杆的力是斜向上的,而外力p始终就是向下,这样的话ab杆的受力的水平分量肯定需要bc杆来平衡,所以bc杆肯定不会是0杆,bc的受力应该可以用平衡方程列出求解。 ) ^1 v6 I. t0 f, A0 Y" E
|||( r w% H* k+ N8 n
zqlei1980 wrote:......bc的受力应该可以用平衡方程列出求解。似乎很难,因为很难求出角度。个人认为这道题其实是理想状态,现实世界中BC肯定不是0杆,除非AB的抗拉刚度为BC的无穷倍,这样BC才是0杆——不知是否正确。 9 \: o, _2 C+ E0 K1 e
|||8 v/ D0 s' o4 A+ K2 H# H$ A7 b8 _
叮铛门铃 wrote:似乎很难,因为很难求出角度。个人认为这道题其实是理想状态,现实世界中BC肯定不是0杆,除非AB的抗拉刚度为BC的无穷倍,这样BC才是0杆——不知是否正确。小变形分析,都假设δ<<L,故该方法都是转角δ\\\"sinδ\\\"tanδ,cosδ\\\"1.在这个假设下,BC杆分到的水平分量(由于向右下位移,三者成静力学的普通节点)非常小,忽略不计.如要象大家讨论的,假设已有某变形后,其实还未平衡(BC杆实际有力),那么要进行第二次迭代,逐渐逼近,如变形不是线性,也许不会收敛,那是杆系有限元分析:要考虑单元内受力符合物理定理,几何变形协调,边界条件....再就还要分析杆件的受力特性是否线性,需要多少次迭代...啊累不累啊?看看有限元的书吧. |
|